今日から始める電子工作xAI 
Youtube
0:00 オープニング
0:24 オームの法則とは
1:15 直列接続と並列接続
2:22 実例:電子工作の回路での使い方
5:13 ワンポイントアドバイス
5:50 まとめ
電子工作初心者のためのオームの法則の使い方
オームの法則とは
オームの法則とは回路を動作させる前に、電流や電圧を事前に予測するための計算式です。
回路を安全且つ正確に動作させるためには必須の知識となります。
オームの法則は
V(電圧)=R(抵抗)×I(電流)
で表すことができます。
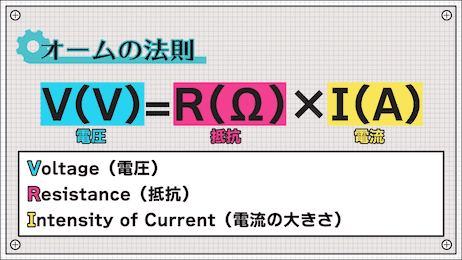
上記の図のように、VはVoltage（電圧）、RはResistance（抵抗）、IはIntensity of Current（電流の大きさ）の略称となっています。
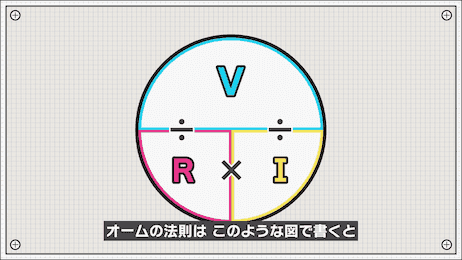
単純にV=IRで暗記しても良いですが、上記の図のようにイメージすると計算のときに分かりやすいです。
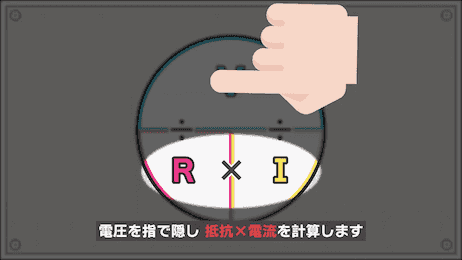
電圧（V）を求めたいときは、求めたい値である電圧を指で隠して、抵抗（R）と電流（I）を乗算します。
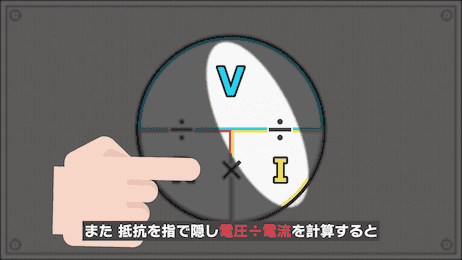
また、抵抗（R）を求めたいときは抵抗を指で隠し、電圧（V）を電流（I）で除算することで抵抗を求めることができます。
直列接続と並列接続
回路の電流、電圧を計算をするためにはオームの法則とセットで覚えておかなくてはいけないルールが直列接続と並列接続の関係です。
部品の接続方法には直列接続と並列接続の2種類があり、どんな回路も基本的には直列と並列の組み合わせによって成り立っています。
また、各部の電流と電圧は、直列か並列かどちらの接続方法で組まれているかで変わってきます。
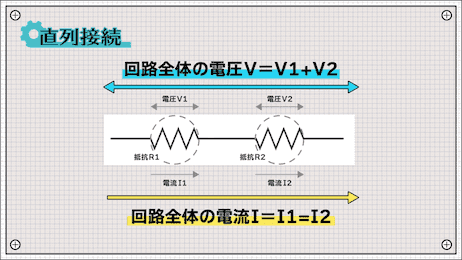
直列接続のときの回路全体の電圧は
回路全体の電圧（V）＝V1＋V2
で表されます。
また回路全体の電流は
回路全体の電流（I）＝I1＝I2
で表され、全て等しくなります。
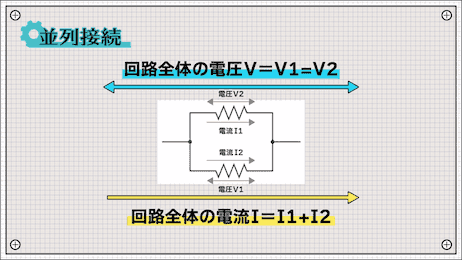
一方で並列接続のときは直列接続のときと関係が逆転します。
回路全体の電圧（V）＝V1＝V2
となり、各部の電圧と等しくなります。
一方で電流の関係は
回路全体の電流（I）＝I1＋I2
で表されます。
以上の直列接続の並列接続の関係性をまとめたものがこちらです。
これらは式だけで覚えようとはせずに、電流が水の流れと同じ性質であるというように
イメージして覚えると覚えやすくなると思います。
実例：電子工作の回路での使い方
オームの法則と基本ルールを覚えたところで、電子工作の回路での使い方を計算してみましょう。
問題1
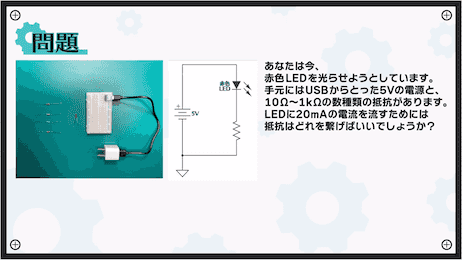
まずはこちらの例題です。
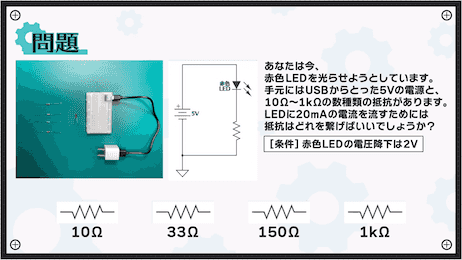
四択となりますが、どれが正解でしょうか。一度考えてみてください。
正解は１５０Ωです。
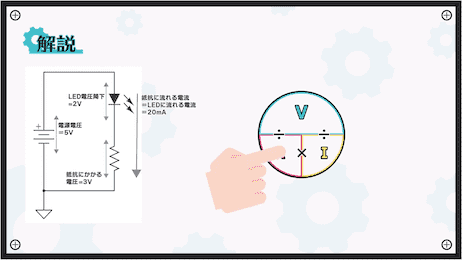
今回の方式で求めたいのは抵抗です。
先ほどの公式の中で、抵抗を隠すことで電圧÷電流となることがわかります。
そこでまず、電圧を求めます。
抵抗にかかる電圧
＝電源電圧-LEDの電圧降下
＝5V-2V
＝3V
となります。
次に電流です。
抵抗に流れる電流
＝LEDに流れる電流
＝20mA
したがって、これらを式に当てはめると
抵抗両端の電圧÷抵抗に流れる電流
＝3V÷20mA
＝150Ω
150Ωが正解となります。
問題2
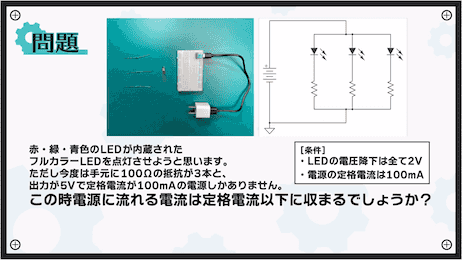
なお定格電流とはそれ以上流してはいけない電流のことです。
また、LEDの電圧降下は全て2Vと仮定します。
定格電流以下に収まるか収まらないか。これも一度考えてみてください。
正解は定格電流以下に収まるです。
それでは解説です。
今度は並列接続となるので、電源に流れる電流は各ルートの電流I1、I2、I3を足したものになります。
I=I1＋I2＋I3
そして各部の電流を求めるときは先ほどのオームの法則の公式の電流を隠します。
すると電圧÷抵抗となることがわかるかと思います。
まずは電圧を求めます。
抵抗にかかる電圧
＝電源電圧-LEDの電圧降下
＝5V-2V
=3V
抵抗値は100Ωとなっているので
抵抗に流れる電圧÷抵抗
=3V÷100Ω
=30mA
これで各ルートにかかる電流は30mAとなります。
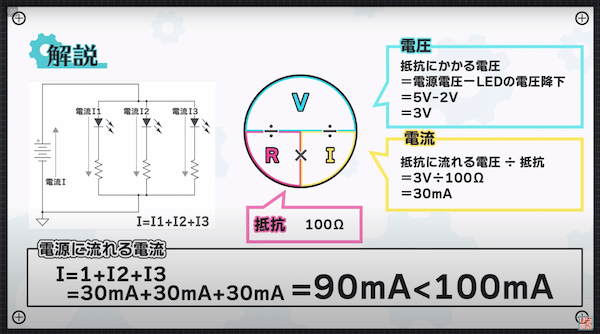
電源に流れる電流は、全ての回路を足したものなので
I
=I1＋I2＋I3
=30mA＋30mA＋30mA
=90mA ＜ 100mA
100mAよりも導いた値が小さくなっているので、定格電流以下に収まることがわかりました。
オームの法則の覚えかた
最後にオームの法則の覚えかたのアドバイスです。
覚えかたのコツは「仮面ライダー」です。
上記の図のように、上にあるVは仮面ライダーの角。
下にあるRとIは仮面RIderのRとIと覚えます。
仮面ライダーとして覚えることで、今回のこの公式は忘れることはないでしょう。
まとめ
今回は「電子工作初心者のためのオームの法則の使い方」というテーマで
オームの法則について解説しました。
いきなり実際の回路で実践するのが怖いという人は
LTspiceのようなシミュレーションを活用するのも一つの手です。
慣れてしまえ難しくないので、そちらも合わせて挑戦してみてはいかがでしょうか。
＼電子工作歴9年の私のイチ押し！ELEGOOの電子工作キット／
